一致性Hash算法-RingHash

发表于 2018-09-12 更新于 2024-06-27 分类于 Algorithm ， ConsistentHash Waline：阅读次数：本文字数： 4.3k 阅读时长 ≈ 7 分钟

哈希环法是最常用的、最经典的一致性哈希算法，也叫做割环法。这个算法易于理解、应用广泛（例如亚马逊的Dynamo¹），实现了最小化的重新映射。

RingHash

按照常用的hash算法来将对应的key哈希到一个具有 $2^{32}$ 次方个桶的空间中，即 $0 \backsim 2^{32}-1$ 的数字空间中。现在我们可以将这些数字头尾相连，想象成一个闭合的环形。
将所有槽位(或者节点) N0,…,Nn−1的标号 0,…,n−1依次作为 hash函数的输入（一般情况下对机器的hash计算是采用机器的IP或者机器唯一的别名作为输入值）进行哈希，把结果分别标记在环上。
对于关于 k的映射，求出 z=hash(k)，标记在环上：
1. 如果 z正好落在槽位上，返回这个槽位的标号。
2. 否则，顺时针沿着环寻找离 z最近的槽位，返回槽位标号。

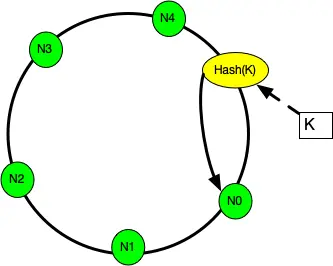
通过上图可以看出对象与机器处于同一哈希空间中，key按顺时针转动找到对应的机器。在这样的部署环境中，hash环是不会变更的，因此，通过算出对象的hash值就能快速的定位到对应的机器中，这样就能找到对象真正的存储位置了。

普通hash求余算法最为不妥的地方就是在有机器的添加或者删除之后会照成大量的对象存储位置失效，这样就大大的不满足单调性了。下面来分析一下一致性哈希算法是如何处理的。

当往一个哈希环中新增一个槽位时，如下图， N5是新增的槽位。可以看到 k从 N0重新映射到了 N5, 而 k1的映射结果不变。稍加分析可以知道，只有被新增槽位拦下来的 k的映射结果是变化了的。新增槽位拦截了原本到下一节点的部分映射，其他槽位不受影响。顺时针方向的下一个节点 N0需要迁移部分数据到新节点N5上才可以正常服务，其他节点不受影响。

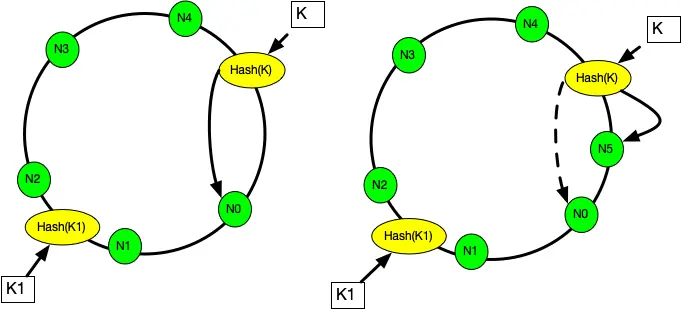
当从一个哈希环中移除一个槽位时，如下图中，N5是被删除的槽位。可以看到 k从 N5重新映射到了 N0，而 k1的映射结果不变。被删除槽位的映射会转交给下一槽位，其他槽位不受影响。顺时针方向的原本映射到 N1的请求会被转交到顺时针方向的下一个节点 N3处理，所以需要迁移 N5的数据到 N0才可以正常服务，其他节点不受影响。

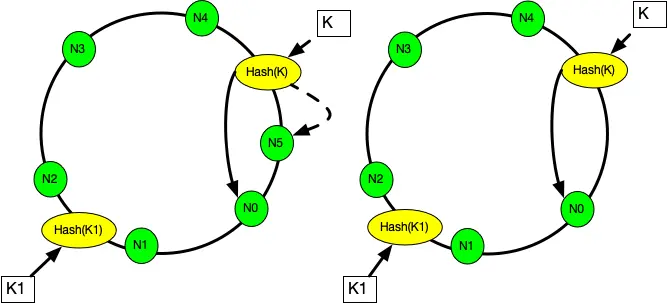
通过对节点的添加和删除的分析，一致性哈希算法在保持了单调性的同时，还使数据的迁移达到了最小。当机器的数目变化时，只会影响到增加或删除的那台机器所在的环的邻接机器的数据存储，而其他机器上的数据不受影响。这样的算法对分布式集群来说是非常合适的，避免了大量数据迁移，减小了服务器的的压力。

根据上面的图解分析，一致性哈希算法满足了单调性和负载均衡的特性以及一般hash算法的分散性，但这还并不能当做其被广泛应用的原由，因为还缺少了平衡性。下面将分析一致性哈希算法是如何满足平衡性的。hash算法是不保证平衡的。在一致性哈希算法中，为了尽可能的满足平衡性，其引入了虚拟节点。虚拟节点(virtual node)是实际节点在 hash空间的副本，一个实际节点（机器,颜色相同）对应了若干个虚拟节点，这个对应个数也成为副本个数，虚拟节点在hash空间中以hash值排列。

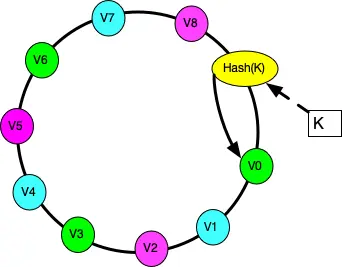
一般，虚拟节点会比物理节点多很多，并可均衡分布在环上，从而可以提高负载均衡的能力:

如果虚拟机器与物理机器映射得好，某一台物理机器宕机后，其上的数据可由其他若干台物理机器共同分担。
如果新添加一台机器，它可以对应多个不相邻环段上的虚拟节点，从而使得hash的数据存储得更分散。
实际应用中，还可以对机器节点添加权重，权重越大的节点，虚拟节点越多，被选中的概率就越大。

哈希环的复杂度分析

哈希环的核心逻辑是如何在环上查找到对应值所在的槽位。这是二分查找可以解决的事情，所以哈希环的映射函数的时间复杂度是 $O(logmn)$ 。对于空间复杂度，显然是 $O(mn)$ . 其中m是虚拟节点的个数。

一致性哈希环算法的映射结果仍然不是很均匀，当有100个虚拟节点时。哈希环法的映射结果的分布的标准差大约有 10%。当虚拟节点增加到1000个时，这个标准差降到 3.2%左右。但很显然，扩大虚拟节点数的，会导致时间和空间复杂度的增长。虚拟节点是一个绝妙的设计，不仅提高了映射结果的均匀性，而且为实现加权映射提供了方式。但是，虚拟节点增加了内存消耗和查找时间。

一致性哈希环下的热扩容和容灾

对于增删节点的情况，哈希环法做到了增量式的重新映射，不再需要全量数据迁移的工作。但仍然有部分数据出现了变更前后映射不一致，技术运营上仍然存在如下问题：

扩容：当增加节点时，新节点需要对齐下一节点的数据后才可以正常服务。
缩容：当删除节点时，需要先把数据备份到下一节点才可以停服移除。
故障：节点突然故障不得不移除时，面临数据丢失风险。

如果我们要实现动态扩容和缩容，即所谓的热扩容，不停止服务对系统进行增删节点，可以这样做：

数据备份(双写)：数据写入到某个节点时，同时写一个备份(replica)到顺时针的邻居节点。
请求中继(代理)：新节点刚加入后，数据没有同步完成时，对读取不到的数据，可以把请求中继(replay)到顺时针方向的邻居节点。

下面的图中演示了这两种规则：

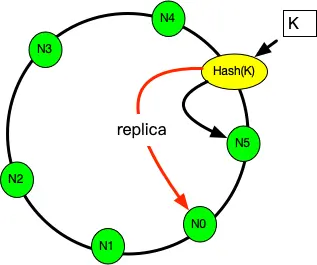
移除节点的情况：每一个节点在执行写请求时，都会写一个备份到顺时针的邻居节点。这样，当 N5节点因故障需要踢除时，新的请求会交接给它的邻居节点 N0， N0上有 k的备份数据，可以正常读到。

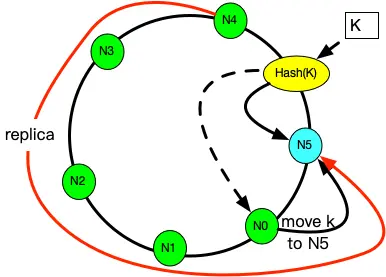
新增节点的情况：对于新增节点的情况稍微复杂点，当新增节点 N5时:
- N5需要从邻居节点 N1上同步部分数据，在同步仍未完成时，可能遇到的请求查不到数据，此时可以先把请求中继给 N1处理, 待两个节点数据对齐后，再结束中继机制。
- N5节点需要从前一邻居N4节点备份数据。

另外，可以备份不止一份。例如备份两次情况，每个写请求都将备份同步到顺时针方向的最近的两个节点上。这样就可以容忍相邻的两节点损失的情况，进一步提高了系统的可用性。中继也可以不止一次。如果一个节点上查不到数据，就中继给下一个节点，最多两次中继，这样就可以满足同时添加”两个正好在环上相邻的”节点的情况了。

算法实现

github 地址

/**
 * hash 环实现一致性hash
 */
public class RingHash {

    /**
     * 真实节点对应的虚拟节点默认值.
     */
    private static final int DEFAULT_VIRTUAL_NODE_COUNT = 1000;

    /**
     * 真实节点对应的虚拟节点数.
     */
    private final int vNodeCount;
    /**
     * 一致性Hash环
     */
    private final SortedMap<Long, VirtualNode> ring;
    /**
     * Hashing function .
     */
    private final HashFunction hashFunction;

    /**
     * hash 环构造器
     *
     * @param hashFunction 内部使用的hash 方法
     */
    public RingHash(HashFunction hashFunction) {
        this(DEFAULT_VIRTUAL_NODE_COUNT, hashFunction);

    }

    /**
     * hash 环构造器
     *
     * @param vNodeCount   真实节点对应的虚拟节点数.
     * @param hashFunction 内部使用的hash 方法
     */
    public RingHash(int vNodeCount, HashFunction hashFunction) {
        this.ring = new TreeMap<>();
        this.vNodeCount = vNodeCount;
        this.hashFunction = hashFunction;
    }

    /**
     * 基于key找到对应的机器节点.
     *
     * @param key
     * @return
     */
    public Node getNode(String key) {
        // 使用设置的hash方法获取key的hash值
        final long keyHash = hashFunction.hash(key);
        final SortedMap<Long, VirtualNode> tailMap = ring.tailMap(keyHash);
        // 在ring上查找
        final Long nodeHash
                = !tailMap.isEmpty()
                ? tailMap.firstKey()
                : ring.firstKey();
        return ring.get(nodeHash).getPhysicalNode();
    }

    /**
     * 向一致性hash中添加节点
     *
     * @param pNode
     */
    public Collection<VirtualNode> addNode(Node pNode) {
        final List<VirtualNode> vNodes = new LinkedList<>();
        for (int i = 0; i < vNodeCount; i++) {
            long hash = hashFunction.hash(pNode.name(), i);
            while (ring.containsKey(hash)) {
                hash = hashFunction.hash(hash, i);
            }
            // 创建虚拟节点
            final VirtualNode vNode = new VirtualNode(pNode, hash);
            ring.put(hash, vNode);
            vNodes.add(vNode);
        }
        return vNodes;
    }

    /**
     * 从一致性hash中删除节点
     *
     * @param toRemove
     */
    public void removeNodes(Collection<VirtualNode> toRemove) {
        for (VirtualNode vNode : toRemove) {
            ring.remove(vNode.getHash());
        }
    }
}

参考

[1] Dynamo: Amazon’s Highly Available Key-value Store